畢氏定理教學網站上網摟!!

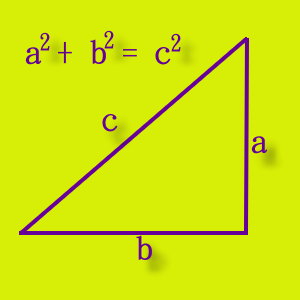
畢氏定理
畢式定理是由畢達哥拉斯發現的，在中國也有人發現，又稱商高定理，
? ? 直角三角形的2股平方和＝斜邊的平方　
? ? 等腰三角形三邊比是１：１：根號２
所謂的畢氏定理就是在一個直角三角形中，斜邊的平方等於兩股平方和，也就是圖中藍色正方形的面積等於黃色加上紅色正方形的面積。　
從畢達哥拉斯時代到現在，畢氏定理已經被提出了許多證明，它已經四百多種不同的證明，甚至於曾經有一位美國總統在他擔任議員的時候也給出一個證明。
畢氏定理揭示了直角三角形三邊之間的度量關係，是直角三角形中的一個重要性質，直角三角形ABC中，a2+b2=c2。因我國古代學者把直角三角形的較短直角邊稱"勾"，較長直角邊稱"股"，斜邊稱"弦"，所以把這個定理稱"畢氏定理"。畢氏定理是一個十分重要而著名的定理，它不僅在數學中有廣泛的應用，而且在其他自然學科，如物理、力學中也常常用到。畢氏定理的發現和證明是我國在幾何學上的一項重要成就。我國古代數學名著《周髀算經》第一章就記載了西周開國時期（約西元前1000年），已發現"勾廣三、股修四、徑隅五"這個畢氏定理的特例。該收又度載了"勾、股各自乘並而開方除之，得邪（同科）至日"，這就是畢氏定理的一般敘述，另一部古算書《九章算術》?也有同樣的記載。

我們小組的畢氏定理教學網站上網摟!!網址在 http://163.20.157.31/triangle 請大家告訴大家喔!!

網站中除了可以看到眾美女的照片外, 並請同學依照小組對於商高定理這個主題，進行同儕評鑑與自我評鑑, 能查出中國及西方商高定理的來源, 並提供多樣的驗證及不同的證明方法.

栽個大跟斗

上一次課程評鑑報告，被教授批得「體無完膚」，使平時自信滿滿的我，深受打擊。沒有想到後果如此不堪，這次我完全是「閉門造車」，以為已經懂得該如何做課程評鑑了，結果，原來搞錯方向。經過這次的經驗，讓我知道，「做學問」還是要紮實一點，該多看看一些書了，免得三年級論文寫不出來，希望這次是「塞翁失馬，焉知非福] ---讓自己在做學問方面更為在成長。

如何修改ｇｏｏｌｇｅ的部落格畫面

真是愈來愈有心得了，為了加入好友的網址於自己的部落格中，以方便閱讀，意外發現，其實在範本中，其實可以改許多東西，如改成中文的畫面，因為其中，有太多英文的設定，不ｆｒｉｅｎｄｌｙ，改成中文較親切。我可要花時間好好改改了。
在此也謝謝郝老師，給了我們這個機會來製作屬於自己的部落格，若非這個「作業」使然，我想我們大概很難「跨出」第一步來製作部落格，還真跟不上這個時代呢！
只是希望，多一點人來點閱，才有勁多寫些東西了。

如何將他人的部落格地址加人自己的部落格!

------號外-------

自己的部落格乏人問津，固然是太少留言，再者也是因為google的部落格不像yahoo的部落格可以訂閱他人的部落格方便。

因此，我就想要如何在自己的部落格中可以方便連結到他人的部落格中呢。經多方研究及"高人指點"，終於達成了!!!!

希望從此，大家可以更方便互通有無了。

方法如下:

1、選擇範本

2、找到以下html(請按圖索驥…)改"Links"的地方

3、加入同學的網艗：ａ、先複製一行同樣的網址，再改上同伴的網址

4、存檔/發佈(記得發佈喔，否則看不到新的網址)

祝大家成功!

學校的道德教育是必須的!!加油加油

這一篇雖然只是笑話,但是小朋友尊師重道的思想的確已經不一樣了,我自己的班上課時多多少少都會趁機提到一些道德問題讓學生討論及引導,希望....大家加油喔!!!

*阿扁向人民報告 之 校園後遺症
------------------------------------------------------------------------
? 老師 : 小明，有同學檢舉你上禮拜五考試時作弊！
? 小明 : 你不要污衊我，我是班長，我有高道德標準，我會作弊嗎？如果你能提出證據證明我作弊，我就自動退學！
? 老師 : 這不就是你的小抄嗎？
? 小明：我身為班長、每天要處理很多班上的事，讀書時間難免不夠，但我還是堅持服務大家、自己再熬夜讀書
? 老師：我再問你一次，這是不是你的小抄？如果是的話，依校規，你恐怕要被退學…
? 小明：我個人的去留微不足道，但是如果因為我被栽贓作弊，害得班上的名聲被糟蹋掉，叫同學出去怎麼做人？
? 老師：好吧！看你一直顧左右而言它的樣子，顯然這小抄就是你的了…
? 小明 : 不！這不是我的，是甲君的！
? 老師 : 甲君是誰？
? 小明 : 身為班長，我要有義氣，不能因為要自保自清，就出賣同學，害同學被扣分，我寧願被冤枉也不可以說！老師 : 可是這上面的筆跡明明是你的！你的字跡很好認！小明 : 你用膝蓋想也知道，我不用作弊也有60分，我有必要為了多個5分10分去作弊，害自己被退學嗎？我會歪哥嗎？
? 老師 : 作弊就是不對！
? 小明 : 你有調查過全校2000名同學中的其他1999人都沒有作弊嗎？去年剛畢業的學長小華就有作弊，你為什麼不抓他？
? 老師 : 我現在抓到你作弊當然要處理，這跟其他同學沒有關係！
? 小明：我三年來都這麼做，你為什麼一開始不跟我講考試不能帶小抄？到現在才出來說我作弊！
? 老師：因為老師之前都信任大家，不刻意去抓，但今天有同學檢舉了，老師不得不辦！
? 小明：好！我再說一次，如果下次你當場抓到我作弊，我就自動退學
? 老師：你剛才不是說，如果我能提出你作弊的證據，你就自動退學嗎？
? 小明：那是〝間接〞抓到，不算！如果你〝直接〞當場抓到，我就服氣。
? 老師：作弊就作弊，還有分直接、間接的嗎？
? 小明 : 老師你是外省人喔？
? 老師 : ？？？
? 小明 : 我阿公在二二八事件中被國民黨的軍隊打死、我爸在美麗島事件中也被抓去關，你們外省人都愛欺負我們台灣人！老師 : 我是本省人耶！
? 小明 : 那你一定是中共派來台灣臥底的台奸，中共的同路人、賣台集團的一份子、你滾回大陸啦！
? 老師 : 算了！老師不處罰你了，小明，你好好作弊，你以後一定可以當總統的Orz

其實遺忘是必要的 洪蘭

其實遺忘是必要的 洪蘭
台灣現在很注重孩子的記憶，忽略了孩子的紀律，這其實很危險。就將來成功的條件來說，紀律遠比記憶重要……洪蘭我去朋友家，發現她的女兒才兩歲就很會幫忙做事，她坐在客廳跟我聊天，需要筆寫東西時就跟女兒說：「妹妹，去書房幫媽媽拿枝筆來。」女兒就快快的拿來，等一下又說：「妹妹，去臥房把媽媽的皮包拿來。」女兒又快快的拿來，用完了，自己會放回去。看得我目瞪口呆，她笑著說：「你忘記『心理學』裡『學習』那一章了嗎？學習就是個連結呀！只要所有東西都有固定地方放，很小的小孩都可以使喚去做事。」的確，一個孩子如果聽得懂那個物件的名稱，又知道那個物件放置的地點，就可以輕鬆地拿到那個東西。如果從小養成孩子物歸原位的習慣，他以後就不必浪費時間找東西，紀律是成功的要件之一，有紀律才有毅力，才會成功。
我們平常會找不到東西是因為生活習慣不好，東西亂放，增加回憶時提取線索的干擾（老太太出門時，把金子換了三個地方藏，回來後就找不到了），如果剪刀永遠放在廚房的第一個抽屜，那麼，剪刀和抽屜就形成強壯連結，一想到剪刀，就想到抽屜，就不會找不到了。也就是說，如果每樣東西都有固定的地方放置，就不必花大腦資源去記哪樣東西放在哪哩，大腦資源就可以釋放出來去記別的事，生活就會有效率。
所以良好的生活習慣，是成功的第一步。東西有固定地方放的另一個重要性是別人不會誤拿，前幾年台灣有個醫院把放鬆肌肉的藥物跟三合一疫苗放在一起，結果護士誤替嬰兒注射放鬆肌肉的針，導致嬰兒死亡，所以培養良好的習慣比教導知識還更重要。很多人一找東西就以為是自己記憶不好，以為記憶好，一切都美好，其實遺忘是必要的，如果一個人什麼都不遺忘，那麼他無法成大事，因為細節塞滿了他的注意力系統，所謂「拘小節者不能成大事」。
俄國的心理學家盧瑞亞（Aleksandar Luria）曾經研究一個完美記憶的人，這個人在看一眼很長的數學公式之後，經過十五年，仍然可以一字不誤的背誦出來，但是他的生活痛苦極了，不相干的訊息一直湧出來，干擾他處理現在的訊息，使他最後一事無成，潦倒終身。所以很多時候，遺忘是個福氣，很多事不必記掛在心頭，過去的就算了，遺忘和選擇性記憶是大自然使人可以繼續活下去的一個重要機制，我們選擇對我們重要的東西去注意，忘記使自己痛苦的事。台灣現在很注重孩子的記憶，忽略了孩子的紀律，這其實很危險。就將來成功的條件來說，紀律遠比記憶重要。在孩子小的時候，花時間培養他良好的生活習慣，比送他去補習班更有幫助，因為紀律會使他以後一生受用不盡。
【2006-05-13/聯合報/E7版/聯合副刊】
讀了上述的文章，是於我心有戚戚焉！我一直也不贊成家長總是把小孩送到補習班去，造成孩子對生活價值的偏差思想，他們以補習班為主，卻以學校生活為輔，尊重（怕比較恰當）補習班的老師，在那哪?用功讀書，但在學校卻不以為意，以班上上課的教室為遊樂場，不把老師上課的內容及考試放在眼?，在學校和同學聯絡感情為樂，這樣真的是本末倒置，但家長也無可耐何，因為家長要工作，且也無法在功課上管教孩子，所以只好將孩子交給補習班。站在教師的立場，真的也無法再說什麼，這不也是整個社會結構的問題嗎？多元文化、潛在課程的觀念讓我更加用不一樣的看法來對待這些學習較弱的同學，有時也不忍苛責他們，畢境他們無法像家境優渥的人可以在各方面加強孩子，讓他們不輸在起跑點，更不會輸在跑道上。